Global Optimisation of Neural Network Models Via Sequential Sampling-Importance Resampling

João F.G. de Freitas - Sue E. Johnson - Mahesan Niranjan - Andrew H. Gee

Cambridge University Engineering Department
Trumpington Street, Cambridge CB2 1PZ, UK.
email { jfgf, sej28, niranjan, ahg }

• 1. Introduction
• 2. State Space Neural Network Modelling
• 3. Sequential Sampling-Importance Resampling
• 4. Experiments
  • Expt 1: Non-linear Modelling
  • Expt 2: Latent States Estimation
• 5. Conclusions
• References

We propose a novel strategy for training neural networks using sequential Monte Carlo algorithms. This global optimisation strategy allows us to learn the probability distribution of the network weights in a sequential framework. It is well suited to applications involving on-line, nonlinear or non-stationary signal processing. We show how the new algorithms can outperform extended Kalman filter (EKF) training.

1 INTRODUCTION

This paper addresses sequential training of neural networks using powerful sequential sampling techniques. Sequential techniques are important in many applications of neural networks involving real-time signal processing, where data arrival is inherently sequential. Furthermore, one might wish to adopt a sequential training strategy to deal with non-stationarity in signals, so that information from the recent past is lent more credence than information from the distant past.

One way to sequentially estimate neural network models is to use a state space formulation and the extended Kalman filter [7]. This involves local linearisation of the output equation, which can be easily performed, since we only need the derivatives of the output with respect to the unknown parameters. This approach has been employed by several authors, including ourselves. Recently, we demonstrated a number of advanced ideas in this context using a hierarchical Bayesian framework [1]. In particular, we proposed ways of tuning the noise processes to achieve regularisation in sequential learning tasks.

However, local linearisation leading to the EKF algorithm is a gross simplification of the probability densities involved. Nonlinearity of the output model often induces multi-modality of the resulting distributions. Gaussian approximation of these densities will lose important details. The approach we adopt in this paper is one of sampling. In particular, we propose the use of `sampling-importance resampling' [5, 8] and `sequential importance sampling' [3, 4, 6] algorithms to train multi-layer neural networks.

2 STATE SPACE NEURAL NETWORK MODELLING

As in our previous work, we start from a state space representation to model the neural network's evolution in time. A transition equation describes the evolution of the network weights, while a measurements equation describes the nonlinear relation between the inputs and outputs of a particular physical process. In mathematical terms:

wk+1	= wk + dk	(1)
yk	= g( wk , xk ) + vk	(2)

where ( ) denotes the output measurements ( ) the input measurements and
( ) the neural network weights. The measurements nonlinear mapping g(.) is approximated by a multi-layer perceptron (MLP). It is widely known that this neural model exhibits the capacity to approximate any continuous function, to an arbitrary precision, as long as it is not restricted in size. Nonetheless, the work may be easily extended to encompass recurrent networks, radial basis networks and many other approximation techniques. The measurements are assumed to be corrupted by noise vk which in our case we model as zero mean, uncorrelated Gaussian noise with covariance R.

We model the evolution of the network weights by assuming that they depend on their previous value wk and a stochastic component dk. The process noise dk may represent our uncertainty in how the parameters evolve, modelling errors or unknown inputs such as target manoeuvres. We assume the process noise to be a zero mean, uncorrelated Gaussian process with covariance Q. We have shown previously that the process of adapting Q is equivalent to adapting smoothing regularisation coefficients and distributed learning rates [1]. To simplify the exposition in this paper, we do not treat the problem of estimating the noise covariances and initial conditions. To understand how these variables may be estimated via hierarchical Bayesian models or EM learning, the reader is referred to our previous work [1, 2].

From a Bayesian perspective, the posterior density function p(Wk |Yk ) , where Yk = { y 1 , y 2 , ... , y k } and Wk = { w 1 , w 2 , ... , w k } , constitutes the complete solution to the sequential estimation problem. In many applications, it is of interest to estimate one of its marginals, namely the filtering density p(wk |Yk ) If we know this density, we can easily compute various estimates of the network weights recursively, including centroids, modes, medians and confidence intervals. Given a prior, the filtering density can be computed by:

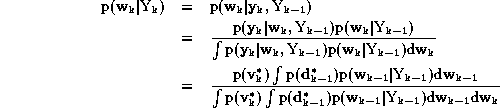
where and .

This optimal solution unfortunately entails multi-dimensional integration, making it impossible to evaluate analytically for most applications. Therefore approximations such as direct numerical integration or Monte Carlo simulation methods are needed.

3 SEQUENTIAL SAMPLING- IMPORTANCE RESAMPLING

In Monte Carlo simulation a set of weighted samples drawn from the posterior density function of the neural network weights is used to map the integrations involved in the inference process to discrete sums. More precisely, we make use of the following Monte Carlo approximation:

where represents the samples used to describe the posterior density and denotes the Dirac delta function. Consequently, any expectations of the form:

may be approximated by the following estimate:

where the samples are drawn from the posterior density function.

A problem arises because often we cannot sample directly from the posterior density function. However, we can circumvent this difficulty by sampling from a known, easy-to-sample, proposal density function and making use of the following substitution:

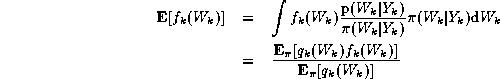
where the unnormalised importance ratios are given by:

In order to compute a sequential estimate of the posterior density function at time k without modifying the previously simulated states Wk-1 , we may adopt the following proposal density:

Consequently, if we assume that the states correspond to a Markov process and that the observations are conditionally independent given the states, it follows that:

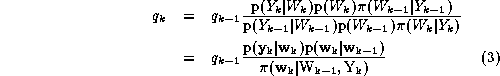
We adopt the following proposal function, likelihood and prior:

Thus we can draw initial weights and importance ratios from the prior (eqn 6) and for each sampling stage, predict the new weights (eqn 1), evaluate the new importance ratios (eqns 3,4,5) and resample if necessary.

Resampling can be performed to concentrate the samples round the areas with a high importance ratio. A uniform random number is mapped onto the cumulative importance distribution and the sampling index corresponding to this point is found. By repeating this S times, the new resampled indices are determined, with the new importance ratios being set to . Clearly, more ``children'' arise from the original samples with the greatest likelihood, with the random variation being added by the subsequent prediction stage. This process will be called Sampling Importance Resampling (SIR) and is illustrated in Figure 1.

Liu and Chen have argued that when all the importance ratios are nearly equal, resampling only reduces the number of distinctive streams and introduces extra variation in the simulations [6]. Therefore, in order to reduce the computational cost of the algorithm, resampling is only performed when the variance of the importance ratio exceeds a certain threshold. This leads to Sampling Importance Partial Resampling (SIPR).

 
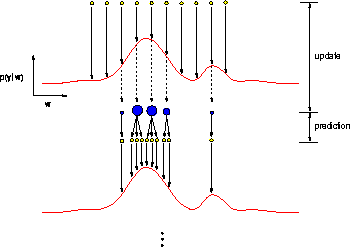
Figure 1: The sequential sampling process. The samples are propagated according to their likelihood found in the update stage. A process noise term is added to the surviving samples and those with higher likelihood are assigned more ``children''. This produces a better weighted description of the likelihood function.

4 EXPERIMENTS

The first experiment compares the use of the described SIR and SIPR techniques with the standard EKF algorithm. This allows the ability of the SIR techniques to handle non-linear models to be seen. The second experiment shows the ability of SIR to find hidden parameters in a simple neural network when the network model is both stationary and non-stationary.

4.1 Expt 1: Non-linear Modelling

where the inputs x1 and x2 where simulated from a Gaussian distribution with zero mean and unit variance. The noise v was generated from a Gaussian distribution with zero mean and standard deviation equal to 0.01. The data was then approximated with an MLP with 5 hidden sigmoidal neurons and a linear output neuron. The MLP was trained sequentially using the SIR, SIPR and EKF algorithms. The threshold for SIPR gave an average of 50% occurrence of resampling. 100 samples were used in the Monte Carlo simulations.

Table 1 shows the average one-step-ahead prediction errors obtained for 10 runs, of 200 time steps each, on a Silicon Graphics R10000 workstation. It is clear from the results that reducing the number of occurrences of resampling does not yield a great reduction in computational time. The results also show the improvements which can be gained by using SIR at the expense of increased computational time.

Expt 2: Latent States Estimation

To assess the capacity of our algorithms to estimate hidden parameters, output data was generated from an MLP, with one sigmoidal hidden unit and a linear output unit. This input consisted of two Gaussian sequences. This is a very simple model, which is only slightly more complex than a logistic data generator and is shown in Figure 2.

  
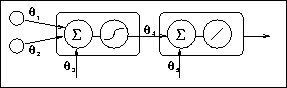
Figure 2: Neural net architecture used for experiment 2.

A second network with the same structure was then trained using the input-output data generated by the first network. Figure 3 shows the performance of the SIR algorithm for a stationary model, both with training data and with data not encountered in the training set. As depicted in Figure 4, the means of the network weights converged to their true value. Figure 4 also shows the error bars (one standard deviation wide) of the estimates. The evolution of the probability density function of the weight of value 1 is plotted in Figure 5. The experiment was then repeated with a non-stationary model, where some of the network weights changed with time. The results are shown in Figure 6.

  
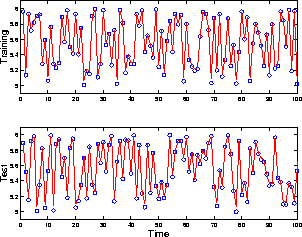
Figure 3: Network prediction on training and test data. Actual output[o o ] and estimated output [--].

  
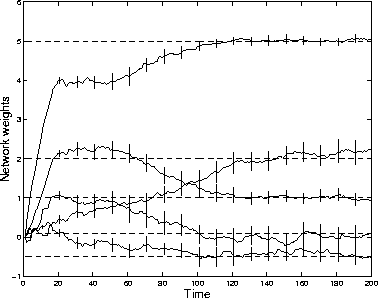
Figure 4: Hidden weights estimation for a stationary model,

  
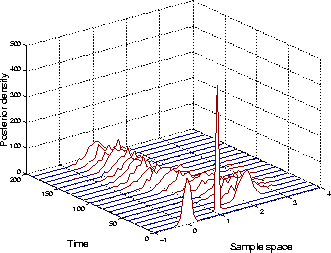
Figure 5: Evolution of the probability density of

  
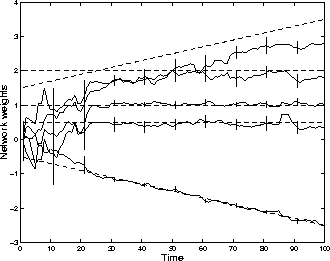
Figure 6: Hidden weights estimation for a non-stationary model,

5 CONCLUSIONS

Our experiments, together with various financial studies presented in [3], clearly indicate that the neural network training algorithms proposed in this paper represent an interesting and promising alternative to existing methods. Sampling methods provide a better description of the probability distribution of the network's weights than conventional second order gradient descent methods, such as the extended Kalman filter. Yet, for problems where the posterior is essentially unimodal, the EKF leads to accurate and much faster algorithms.

Acknowledgements
We would like to thank Neil Gordon (DERA) for his helpful assistance. João F.G. de Freitas is financially supported by two University of the Witwatersrand Merit Scholarships, a Foundation for Research Development Scholarship (South Africa), an ORS award and a Trinity College External Studentship (Cambridge).

References

1

J F G de Freitas, M Niranjan, and A H Gee.
Hierarchichal Bayesian-Kalman models for regularisation and ARD in sequential learning [ ps]
Technical Report CUED/F-INFENG/TR 307, Cambridge University, Dec. 1997

2

J F G de Freitas, M Niranjan, and A H Gee.
The EM algorithm and neural networks for nonlinear state space estimation [ ps]
Technical Report CUED/F-INFENG/TR 313, Cambridge University, 1998.

3

J F G de Freitas, M Niranjan, A H Gee, and A Doucet.
Sequential Monte Carlo methods for optimisation of neural network models [ ps]
Technical Report CUED/F-INFENG/TR 328, Cambridge University, July 1998

4

A Doucet.
On sequential simulation-based methods for Bayesian filtering [ps]
Technical Report CUED/F-INFENG/TR 310, Cambridge University, 1998.

5

N J Gordon, D J Salmond, and A F M Smith.
Novel approach to nonlinear/non-Gaussian Bayesian state estimation
IEE Proceedings-F, 140(2):107-113, April 1993.

6

J S Liu and R Chen.
Sequential Monte Carlo methods for dynamic systems
To appear in the Journal of the American Statistical Association, 1998.

7

S Singhal and L Wu.
Training multilayer perceptrons with the extended Kalman algorithm
In D S Touretzky, editor, Advances in Neural Information Processing Systems, volume 1, pages 133-140, San Mateo, CA, 1988.

8

A F M Smith and A E Gelfand.
Bayesian statistics without tears: a sampling-resampling perspective
American Statistician, 46:84-88, 1992.