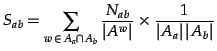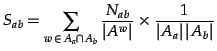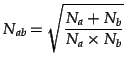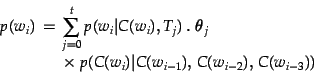Class-based language model adaptation using
mixtures of word-class weights
Gareth
Moore
Steve
Young
glm20@eng.cam.ac.uk sjy@eng.cam.ac.uk
Engineering Department, University of Cambridge
Trumpington Street, Cambridge, CB2 1PZ, UK
Abstract:
This paper describes the use of a weighted mixture of class-based
n-gram language models to perform topic adaptation. By using a fixed
class n-gram history and variable word-given-class probabilities we
obtain large improvements in the performance of the class-based
language model, giving it similar accuracy to a word n-gram model, and an
associated small but statistically significant improvement when we
interpolate with a word-based n-gram language model.
Previously, weighted mixtures of word n-gram language models have been
used to provide a topic adaptation method for large vocabulary speech
recognition [3]. A disadvantage of
this method, however, is that these models require large numbers of
parameters per topic, which in turn necessitates a large quantity of
training data for each topic and associated storage space per topic in
the resulting language model. We investigate an alternative approach
to topic mixtures within the n-gram paradigm by using a class-based
n-gram language model with a fixed class n-gram history but varying
word-given-class probabilities for each topic. By using a weighted
mixture of these word probabilities with a static class history
component we develop a topic-switching language model which uses only
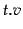 parameters over and above a normal class-based n-gram language
model, where
parameters over and above a normal class-based n-gram language
model, where 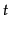 is the number of topics and
is the number of topics and 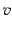 is the vocabulary
size. In addition, due to the nature of the class-based language
model, less training data is required per topic than in the word
n-gram case thus allowing adaptation to be performed with relatively
small amounts of topic-specific text.
A mixture of broadcast news and newswire text was used as training
data for the topic model, with 144 million words of Broadcast News
text and 25 million words of Los Angeles Times/Washington Post (LATWP)
newswire text forming a corpus of 153,886 articles. The existing
corpus article boundaries were treated as indivisible elements for the
purpose of topic-finding.
Article clustering was performed in an unsupervised iterative manner
by repeatedly merging the two articles found to be `most similar'
according to a word co-occurrence metric, until a given number of
article clusters was reached. Each of these groups of articles was
then treated as a distinct topic.
The article clustering method employed was that used in
[2], as based on [4].
Each article is initially placed in a singleton group, and then
given two article groups,
is the vocabulary
size. In addition, due to the nature of the class-based language
model, less training data is required per topic than in the word
n-gram case thus allowing adaptation to be performed with relatively
small amounts of topic-specific text.
A mixture of broadcast news and newswire text was used as training
data for the topic model, with 144 million words of Broadcast News
text and 25 million words of Los Angeles Times/Washington Post (LATWP)
newswire text forming a corpus of 153,886 articles. The existing
corpus article boundaries were treated as indivisible elements for the
purpose of topic-finding.
Article clustering was performed in an unsupervised iterative manner
by repeatedly merging the two articles found to be `most similar'
according to a word co-occurrence metric, until a given number of
article clusters was reached. Each of these groups of articles was
then treated as a distinct topic.
The article clustering method employed was that used in
[2], as based on [4].
Each article is initially placed in a singleton group, and then
given two article groups, 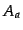 and
and 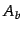 , the similarity between the two
groups,
, the similarity between the two
groups, 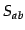 , is defined as
, is defined as
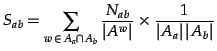 |
(1) |
where 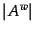 is the number of article groups that contain the word
is the number of article groups that contain the word
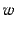 , and
, and 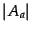 is the number of distinct words in the article group
is the number of distinct words in the article group
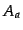 .
. 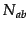 is a normalisation factor defined as
is a normalisation factor defined as
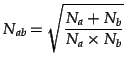 |
(2) |
where 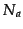 is the number of articles contained within the article
group
is the number of articles contained within the article
group 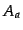 . This normalisation factor is used to stop exceptionally
large clusters from forming and dominating the rest of the clustering
process. All words were considered when clustering, except for an
ignored stop-list of 182 high-frequency function words obtained by
manual examination of a frequency list taken from the corpus used -
this was an attempt to speed up the clustering process based on the
assumption that these high-frequency function words were unlikely to
contribute to the distinctiveness of the topics. For similar reasons
all one and two character words were ignored - this also allowed
optimisation of the hashing algorithm used in the implementation of
this algorithm.
Too many articles were present in the initial corpus for it to be
feasible to perform top-down clustering using the full set (since all
possible pairs must be compared before each single merge operation),
so it was first split into groups of 1000 articles - these 1000
article groups each consisted of articles which followed one another
in the original corpus, meaning that the articles in each group were
generally for a consecutive range of times and dates. Each of these
groups was then clustered from 1000 down to 100 `topics'. This process
was then repeated iteratively in a top-down manner, by using these 100
`topics' as new indivisible `articles' and grouping ten sets of them
into a new initial group of 1000, until the desired number of topics
resulted.
A word 4-gram language model was built using the Broadcast News and
LATWP corpus text, supplemented with 850,000 words of Broadcast News
acoustic text and 100,000 words of Marketplace acoustic text. This
combined corpus, and the eras used, was chosen to match the
text used to train the HTK-system language models built for the HUB-4
1997 evaluation [5] - this allows our new language model to
be experimentally evaluated by rescoring the lattices originally built
for this evaluation (see section 4 below).
Cut-offs of 1, 3 and 3 were used for the bigram, trigram and fourgram
components of the word model respectively. Three similar class-based
4-gram models were also built, for 503, 1003 and 2003 classes. The
sentence start, end and unknown word tokens were kept in singleton
classes. Kneser and Ney's clustering algorithm
[1] was used to decide on the class members, and
two iterations of it were performed for each model. The vocabulary of
65425 words from the original evaluation was used. A fixed ratio of
0.65:0.35 as used for interpolating between word and class models based
on experiments performed rescoring lattices built from the HUB-4 1997
development test set.
Using the topic-clustering algorithm described in section 2, four
differently-sized topic sets were built, consisting of 50, 100, 250
and 500 topics respectively. For each of the topics in each of these topic
sets, word-given-class probabilities were calculated for each of the class
model sizes using the class maps constructed using the full training set
corpus. These topic-specific word probability maps were each then combined
with the class history n-grams calculated using the full training set in
order to form a separate language model for each topic and class size - this
was in addition to the existing `overall' model already constructed for each
number of classes.
Given a fixed number of classes, each model is thus defined by:
. This normalisation factor is used to stop exceptionally
large clusters from forming and dominating the rest of the clustering
process. All words were considered when clustering, except for an
ignored stop-list of 182 high-frequency function words obtained by
manual examination of a frequency list taken from the corpus used -
this was an attempt to speed up the clustering process based on the
assumption that these high-frequency function words were unlikely to
contribute to the distinctiveness of the topics. For similar reasons
all one and two character words were ignored - this also allowed
optimisation of the hashing algorithm used in the implementation of
this algorithm.
Too many articles were present in the initial corpus for it to be
feasible to perform top-down clustering using the full set (since all
possible pairs must be compared before each single merge operation),
so it was first split into groups of 1000 articles - these 1000
article groups each consisted of articles which followed one another
in the original corpus, meaning that the articles in each group were
generally for a consecutive range of times and dates. Each of these
groups was then clustered from 1000 down to 100 `topics'. This process
was then repeated iteratively in a top-down manner, by using these 100
`topics' as new indivisible `articles' and grouping ten sets of them
into a new initial group of 1000, until the desired number of topics
resulted.
A word 4-gram language model was built using the Broadcast News and
LATWP corpus text, supplemented with 850,000 words of Broadcast News
acoustic text and 100,000 words of Marketplace acoustic text. This
combined corpus, and the eras used, was chosen to match the
text used to train the HTK-system language models built for the HUB-4
1997 evaluation [5] - this allows our new language model to
be experimentally evaluated by rescoring the lattices originally built
for this evaluation (see section 4 below).
Cut-offs of 1, 3 and 3 were used for the bigram, trigram and fourgram
components of the word model respectively. Three similar class-based
4-gram models were also built, for 503, 1003 and 2003 classes. The
sentence start, end and unknown word tokens were kept in singleton
classes. Kneser and Ney's clustering algorithm
[1] was used to decide on the class members, and
two iterations of it were performed for each model. The vocabulary of
65425 words from the original evaluation was used. A fixed ratio of
0.65:0.35 as used for interpolating between word and class models based
on experiments performed rescoring lattices built from the HUB-4 1997
development test set.
Using the topic-clustering algorithm described in section 2, four
differently-sized topic sets were built, consisting of 50, 100, 250
and 500 topics respectively. For each of the topics in each of these topic
sets, word-given-class probabilities were calculated for each of the class
model sizes using the class maps constructed using the full training set
corpus. These topic-specific word probability maps were each then combined
with the class history n-grams calculated using the full training set in
order to form a separate language model for each topic and class size - this
was in addition to the existing `overall' model already constructed for each
number of classes.
Given a fixed number of classes, each model is thus defined by:
 |
(3) |
where 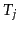 is the
is the 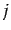 th topic,
th topic, 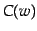 is the class of word
is the class of word 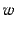 and
and 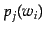 is the probability of the
is the probability of the 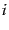 th word given topic
th word given topic 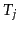 . Note that since not all of the
vocabulary words were seen in every topic, these zero occurrence words
were given a notional count of one when calculating word-given-class
probabilities. Other smoothing methods were tried but this was found
to perform better than various discounting methods attempted.
Although we could perform recognition experiments individually with
each of these topic-specific models, we can construct an adaptable
model by using a mixture of all the models for a given number of
classes and then choosing different weights for each topic. The
models were combined by linear interpolation:
. Note that since not all of the
vocabulary words were seen in every topic, these zero occurrence words
were given a notional count of one when calculating word-given-class
probabilities. Other smoothing methods were tried but this was found
to perform better than various discounting methods attempted.
Although we could perform recognition experiments individually with
each of these topic-specific models, we can construct an adaptable
model by using a mixture of all the models for a given number of
classes and then choosing different weights for each topic. The
models were combined by linear interpolation:
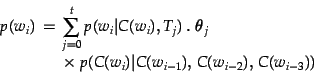 |
(4) |
where 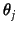 is the weight of topic
is the weight of topic 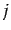 , given that
, given that
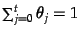 for
for 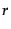 topics.
topics. 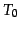 is the overall
`topic' trained on the entire training set.
In order to use this model in an unsupervised manner it is necessary
to devise some automatic way of determining the weights,
is the overall
`topic' trained on the entire training set.
In order to use this model in an unsupervised manner it is necessary
to devise some automatic way of determining the weights, 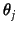 .
Various methods are possible, but in the experiments reported here
they were chosen on the basis of perplexity on recently-seen or
first-pass recognition text.
Recognition experiments were performed by rescoring existing lattices
previously built for the HUB-4 1997 evaluation - these were originally
constructed using a 4-gram word model. We found the 1-best solutions from
each of these lattices and calculated the perplexity of this text using each
of the different topic models (as defined in equation 3) in turn. In one set
of experiments the weights were then set to 0 for all topics except for the
one with the lowest perplexity on the 1-best solution, which was given a
weight of 1. A second set of experiments used the EM algorithm to optimise
the perplexity by iteratively adjusting the weights for each topic - the
iterative step was repeated until the improvement in perplexity was below
0.0001%.
The full HUB-4 1997 evaluation test set was used to assess language
model performance. (Footnote: This set was chosen because of the
existence of a single accurate reference transcription)..
Although the training text
described in section 3 was chosen to try and match the original
training text used to build the HTK system as closely as possible, the
original primary corpora used were unavailable and different text
conditioning was applied to the corpora that were used
instead. (Footnote: This
lead to 105 words from the original 65425-word vocabulary not being
encountered in the training data. To work around this the probability
mass for the unknown word token was evenly distributed amongst these
105 words and the unknown word token itself).
Because of this training
text mismatch the baseline 4-gram word-model lattice 1-best solution
performance of 17.4% word error rate from the original
evaluation rose to 17.6% when rescoring the lattices with the
newly-built 4-gram word model. There were 749 lattices in total,
with an average length per lattice of 43 words.
Experiments were run with all combinations of topic and class size,
with and without use of the EM algorithm for determining the topic weights and with
and without interpolation with a word 4-gram. Word accuracy was
assessed using the NIST scoring tools used for the evaluation. As table
1 shows, the best recognition error rate without using any topic
model, of 17.1%, was obtained by interpolating the 1003 class model with the
word model. Treating this as the baseline result to improve upon,
statistical significance was tested by using the Wilcoxon signed-rank test at
a 5% significance level.
.
Various methods are possible, but in the experiments reported here
they were chosen on the basis of perplexity on recently-seen or
first-pass recognition text.
Recognition experiments were performed by rescoring existing lattices
previously built for the HUB-4 1997 evaluation - these were originally
constructed using a 4-gram word model. We found the 1-best solutions from
each of these lattices and calculated the perplexity of this text using each
of the different topic models (as defined in equation 3) in turn. In one set
of experiments the weights were then set to 0 for all topics except for the
one with the lowest perplexity on the 1-best solution, which was given a
weight of 1. A second set of experiments used the EM algorithm to optimise
the perplexity by iteratively adjusting the weights for each topic - the
iterative step was repeated until the improvement in perplexity was below
0.0001%.
The full HUB-4 1997 evaluation test set was used to assess language
model performance. (Footnote: This set was chosen because of the
existence of a single accurate reference transcription)..
Although the training text
described in section 3 was chosen to try and match the original
training text used to build the HTK system as closely as possible, the
original primary corpora used were unavailable and different text
conditioning was applied to the corpora that were used
instead. (Footnote: This
lead to 105 words from the original 65425-word vocabulary not being
encountered in the training data. To work around this the probability
mass for the unknown word token was evenly distributed amongst these
105 words and the unknown word token itself).
Because of this training
text mismatch the baseline 4-gram word-model lattice 1-best solution
performance of 17.4% word error rate from the original
evaluation rose to 17.6% when rescoring the lattices with the
newly-built 4-gram word model. There were 749 lattices in total,
with an average length per lattice of 43 words.
Experiments were run with all combinations of topic and class size,
with and without use of the EM algorithm for determining the topic weights and with
and without interpolation with a word 4-gram. Word accuracy was
assessed using the NIST scoring tools used for the evaluation. As table
1 shows, the best recognition error rate without using any topic
model, of 17.1%, was obtained by interpolating the 1003 class model with the
word model. Treating this as the baseline result to improve upon,
statistical significance was tested by using the Wilcoxon signed-rank test at
a 5% significance level.
|
Classes |
Word |
Perplexity |
Error rate (%) |
|---|
|
503 |
- |
259.53 |
19.6 |
|---|
|
1003 |
- |
219.77 |
18.5 |
|---|
|
2003 |
- |
194.86 |
18.1 |
|---|
|
- |
 |
174.84 |
17.6 |
|---|
|
503 |
 |
160.54 |
17.3 |
|---|
|
1003 |
 |
160.50 |
17.1 |
|---|
|
2003 |
 |
161.51 |
17.2 |
|---|
|
Table 1: Topic Independent baseline word recognition error rates - a
 in
the column indicates that the class model was interpolated
with a word n-gram model
in
the column indicates that the class model was interpolated
with a word n-gram model
When not interpolating with a word model, significant improvements were
obtained in every case for all sizes of topic model given a fixed number of
classes, with the 250 topic model providing the largest gains, as shown in
table 2. Also in all cases the performance of the EM
algorithm-found topic weights was better than the performance when using the
single best-performing topic (as described at the end of section 3.1), with
the EM algorithm giving larger gains as the number of topics increased,
presumably due to its ability to include more than one of the more
specialised topics; for the same reason the single topic selection method
performed more badly as the number of topics increased.
The results were less clear-cut when interpolating with the word n-gram
model. The only models to obtain a statistically significant improvement were
the two using 50 topics and 1003 classes, with a relative improvement of
1.2%. The models with 50 topics performed best, which was the opposite of
the situation without the word models where the larger topic size of 250 was
favoured. Perhaps this is because the larger local increase in the
probability of low frequency words allowed by a greater number of topics
often occurs in the context of a word sequence which might in itself already
be well modelled by the word model.
Particularly interesting is the fact that the class topic models
perform as well as the word model alone - there is no statistifically
significant difference between the word model performance and that of
any of the 1003 and 2003 class topic models. The 50 topic and
1003 class model has about the same number of parameters as the word
model, but it is far more compact to store since 25% of its 13.5
million parameters are the topic-dependent word counts as opposed to
n-grams, and the range of token ids that must be stored for the
n-grams is 98% less.
|
|
Word error rate (%) |
|
Classes |
Topics |
C+1 |
C+EM |
W+1 |
W+EM |
|
503 |
50 |
19.1 |
18.9 |
17.2 |
17.2 |
|---|
|
1003 |
50 |
18.2 |
18.1 |
16.9 |
16.9 |
|---|
|
2003 |
50 |
17.8 |
17.8 |
17.1 |
17.1 |
|---|
|
503 |
100 |
19.0 |
18.9 |
17.2 |
17.3 |
|---|
|
1003 |
100 |
18.1 |
18.0 |
17.0 |
17.0 |
|---|
|
2003 |
100 |
17.8 |
17.7 |
17.2 |
17.2 |
|---|
|
503 |
250 |
19.1 |
18.8 |
17.3 |
17.3 |
|---|
|
1003 |
250 |
18.3 |
17.9 |
17.0 |
16.9 |
|---|
|
2003 |
250 |
17.9 |
17.7 |
17.2 |
17.2 |
|---|
|
1003 |
500 |
18.3 |
18.0 |
17.0 |
17.0 |
|---|
|
Table 2:
Topic Dependent word recognition error rates. Key:
C - class model only;
W - class model interpolated with word model;
1 - only single best topic used;
EM - multiple topics with weights found using EM algorithm
Although the experiments reported here are concerned with improving
recognition accuracy, it is interesting to examine perplexity figures
too. Table 3 gives figures for the 503 and 1003 class
models, with the perplexity calculated on the reference
transcriptions. As for the lattice experiments, topic weights are
only chosen on lattice/transcription segment boundaries. The 503
class results are shown since they gave the best perplexity results
when interpolated with a word model, and the 1003 class perplexities
are included for comparison because the best recognition results were
obtained with this number of classes. The table omits the
non-EM-weighted results because these are all (by definition) worse
than their EM-weighted equivalent. Improvements through use of
EM-chosen weights are typically around the 4-5% level for models
without word-model interpolation, and around 1% for those with.
Using the 1-best transcription to optimise the log-likelihood clearly
biasses a conventional perplexity measurement so four separate
perplexity measures are presented in table 3, which shows
the performance when picking topics on both the 1-best transcription
and the reference transcription, using either the current or preceding
segment. The final column, therefore, gives the best possible
perplexity results that can be obtained given that the topic cannot
change within a segment. For the preceding segment experiments, the
topic weights for the first segment were set to 1 for the `overall'
model and 0 for all the topic-specific models.
Setting the topic based on the previous, just-seen reference
transcription represents the only `true' perplexity reported here,
since it alone can be calculated without use of recognition
experiments or `cheating'. This works relatively badly, however, with
the largest reduction when interpolating with a word model of 2.2%
obtained using the 503 class model with 50 topics, whilst the best
(1003-class) model for recognition performance gives a 1.5%
reduction. In addition, when topic selection is based on the previous
segment the 250 topic model performs relatively badly, suggesting that
the topic weights are being poorly selected since the lesser numbers
of topics may be performing better simply because this increases the
likelihood of choosing better weights by chance.
By way of contrast, however, the perplexity values when weights are
chosen on the current segment are much lower - this shows that the
model described here can give large perplexity reductions if
the weights are well-estimated, so clearly using the preceding segment
is not very successful. The table also reveals that the
weights which are computed from the lattice 1-best solutions
are relatively close to the best that can be obtained,
suggesting that the method of topic choice used for the
recognition experiments is a good one since it is near to the best
perplexity result that can be obtained - this, however, makes the
assumption that the weights which obtain the best perplexity result
also obtain the best recognition result, which is not guaranteed to be
true. The best improvements in perplexity are obtained by the
250-topic models, in contrast to the best recognition results which
were for the 50-topic models, but the differences in perplexity
between the varying numbers of topics are too small to draw any firm
conclusions.
Examination of the weights selected by the EM algorithm suggests that
the topics constructed by the clustering process are sufficiently
distinct, since for each lattice the vast majority of the weights
are set to zero, with just two or three topics taking over 99% of the
probability mass - this was true even for the 500 topic model. This
suggests that the clustering worked well, and furthermore that the tree
division method did not significantly affect its performance.
It is possible that the clustering method could be improved by
discarding articles that do not fit any topic well, but this has not
been investigated. Experiments were performed on reclustering
the topics on the basis of perplexity using the topic class models,
but this did not lead to any significant improvement in performance.
A method of topic estimation based on scores from the clustering
algorithm rather than on perplexities was also investigated, but this
lead to a decrease in performance.
|
|
Perplexity |
|
|
1-best |
Reference |
|
Classes |
Topics |
W |
Prev |
Curr |
Prev |
Curr |
|
503 |
50 |
- |
254.41 |
220.40 |
252.65 |
216.16 |
|---|
|
503 |
50 |
 |
157.47 |
150.71 |
156.98 |
149.36 |
|---|
|
1003 |
50 |
- |
218.47 |
195.72 |
217.10 |
192.20 |
|---|
|
1003 |
50 |
 |
158.53 |
152.99 |
158.18 |
151.78 |
|---|
|
503 |
100 |
- |
252.01 |
216.86 |
255.54 |
215.25 |
|---|
|
503 |
100 |
 |
157.43 |
149.52 |
157.22 |
148.71 |
|---|
|
1003 |
100 |
- |
220.28 |
193.45 |
218.69 |
189.14 |
|---|
|
1003 |
100 |
 |
158.56 |
151.98 |
158.16 |
150.47 |
|---|
|
503 |
250 |
- |
263.40 |
215.31 |
261.73 |
209.20 |
|---|
|
503 |
250 |
 |
158.00 |
148.52 |
157.44 |
146.53 |
|---|
|
1003 |
250 |
- |
225.85 |
192.66 |
224.24 |
187.37 |
|---|
|
1003 |
250 |
 |
158.98 |
151.15 |
158.68 |
149.37 |
|---|
|
1003 |
500 |
- |
230.96 |
193.86 |
228.93 |
188.11 |
|---|
|
1003 |
500 |
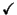 |
159.77 |
151.32 |
159.30 |
149.37 |
|---|
|
Table 3:
Language model perplexities.
Key: Word model interpolated where ticked - class model only where not ticked;
1-best = lattice 1-best text used to choose topics; Reference =
reference transcription used to choose topics; Prev = preceding segment used
in topic estimation; Curr = current segment used in topic estimation
This paper has shown that a small but statistically significant
improvement in word recognition accuracy can be obtained using a
topic-dependent class-based language model with weights computed after
the first pass of a multi-pass recognition strategy. The best overall
results were obtained using 1003 classes and a 50 topic model with
weights optimised using the EM algorithm. Using topic adaptation, a
class-based model can provide equivalent performance to a word-only
model whilst having a much smaller memory footprint.
The form of the model also makes it feasible to perform experiments
using large numbers of topics, such as the 500 used here. In
addition, even with 500 topics the models remain adequately trained,
which suggests that the model described here can also be used to
perform topic adaptation using only small amounts of domain-specific
data.
-
- 1
- R. Kneser and H. Ney,
``Improved clustering techniques for class-based statistical language
modelling''; Proc. Eurospeech 1993, pp. 973-976
- 2
- R. Iyer and M. Ostendorf, ``Modelling Long
Distance Dependence in Language: Topic Mixtures vs. Dynamic Cache
Models''; Proc. ICSLP 1996, Volume 1 pp. 236-239
- 3
- R. Kneser and V. Steinbiss,
``On the Dynamic Adaptation of Stochastic Language Models'';
Proc. ICASSP 1993, pp. 586-589
- 4
- S. Sekine, ``Automatic Sublanguage Identification
for a New Text''; Second Annual Workshop on Very Large
Corpora, Kyoto
- 5
- P.C. Woodland, T. Hain, S.E. Johnson, T.R. Niesler,
A. Tuerk, E.W.D. Whittaker and S.J. Young, ``The 1997 HTK Broadcast
News Transcription System''; DARPA Broadcast News 1998
Transcription and Understanding Workshop