Lossy coding



Next: Compression Performance
Up: SHORTEN: Simple lossless and
Previous: Residual Coding
The previous sections have outlined the complete waveform compression
algorithm for lossless coding. There are a wide range of applications
whereby some loss in waveform accuracy is an acceptable tradeoff in
return for better compression. A reasonably clean way to implement this
is to dynamically change the quantisation level on a segment-by-segment
basis. Not only does this preserve the waveform shape, but the
resulting distortion can be easily understood. Assuming that the
samples are uniformally distributed within the new quantisation interval
of  , then the probability of any one value in this range is
, then the probability of any one value in this range is 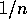 and
the noise power introduced is
and
the noise power introduced is  for the lower values that are
rounded down and
for the lower values that are
rounded down and  for those values that are rounded up. Hence
the total noise power introduced by the increased quantisation is:
for those values that are rounded up. Hence
the total noise power introduced by the increased quantisation is:

It may also be assumed that the signal was uniformally distributed in
the original quantisation interval before digitisation, i.e. a
quantisation error of 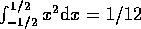 .
.
Shorten supports two main types of lossy coding: the case where every
segment is coded at the same rate; and the case where the bit rate is
dynamically adapted to maintain a specified segmental signal to noise
ratio. In the first mode, the variance of the prediction residual of
the original waveform is estimated and then the appropriate quantisation
performed to limit the bit rate. In areas of the waveform where there
are strong sample to sample correlations this results in a relatively
high signal to noise ratio, and in areas with little correlation the
signal to noise ratio approaches that of the signal power divided by the
quantisation noise of equation 22. In the second mode,
this equation is used to estimate the greatest additional quantisation
that can be performed whilst maintaining a specified segmental signal to
noise ratio. In both cases the new quantisation interval,  , is
restricted to be a power of two for computational efficiency.
, is
restricted to be a power of two for computational efficiency.



Next: Compression Performance
Up: SHORTEN: Simple lossless and
Previous: Residual Coding
Tony Robinson: ajr4@cam.ac.uk
 , then the probability of any one value in this range is
, then the probability of any one value in this range is 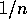 and
the noise power introduced is
and
the noise power introduced is  for the lower values that are
rounded down and
for the lower values that are
rounded down and  for those values that are rounded up. Hence
the total noise power introduced by the increased quantisation is:
for those values that are rounded up. Hence
the total noise power introduced by the increased quantisation is:




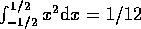 .
.